Convex Set
Definition a line connecting to line in the sets is constrained in the set. The simple terms is we can connect any two points inside the set with a line. In condition that the line which connects the two points is inside the sets.
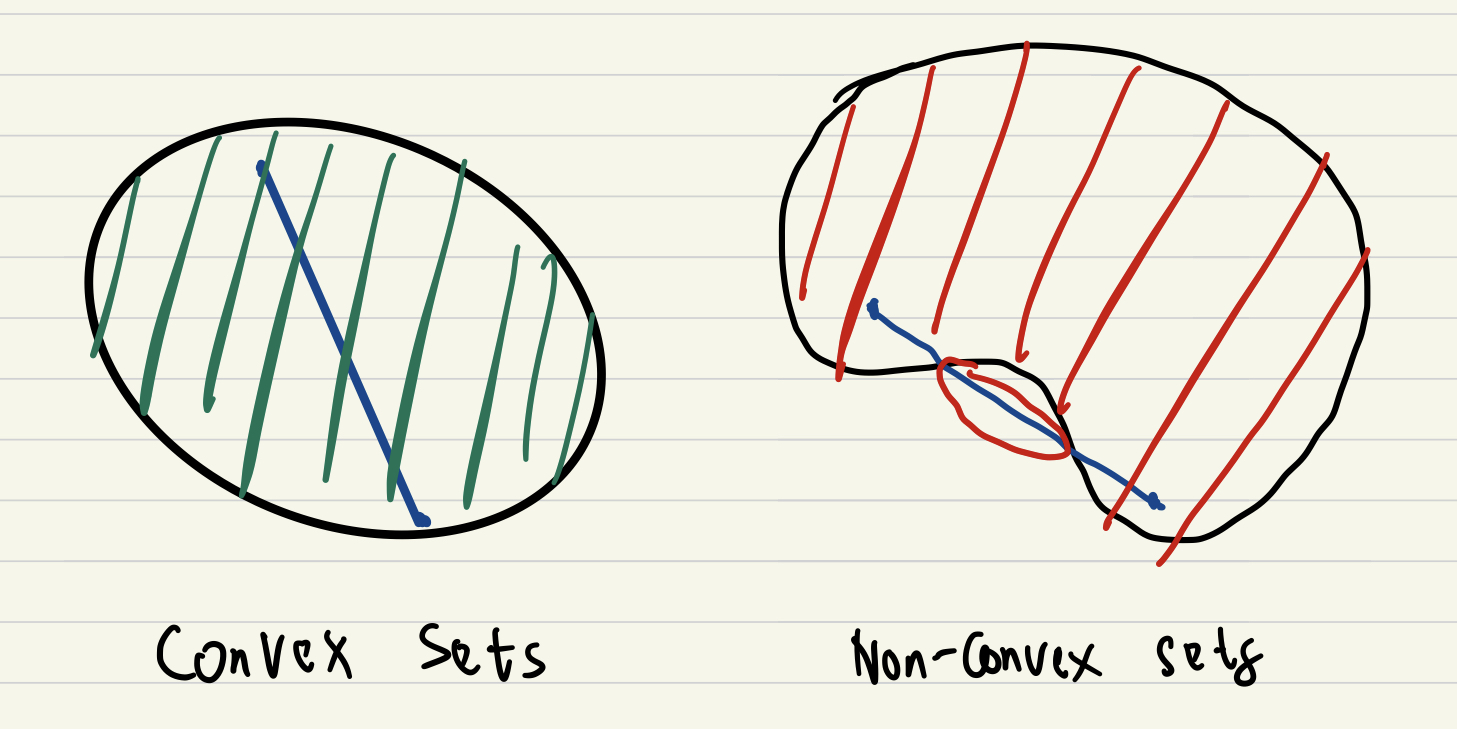
Examples of Convex Sets:
Linear Subspace Ax=bHalf-space, Hyperplane, Polytope Ax≤bElipsoids xTPx≤1,P>0Cones ∥x2:n∥2≤x1
Convex Function
A functionf(x):Rn→Rwhose epigraph is a convex set.
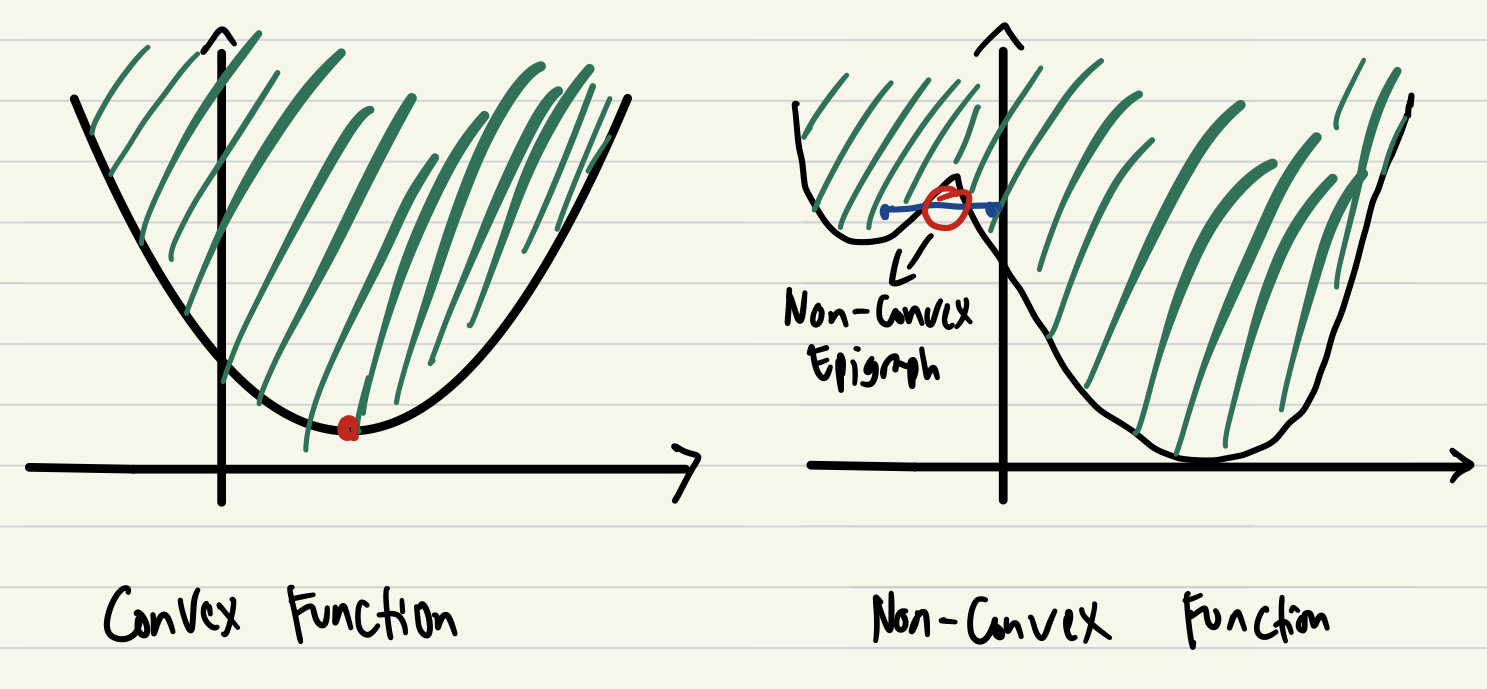
But what is epigraph? Everything above the function lines is called epigraph (dark green hatched area in the figure above).
Examples of Convex Function:
Linear f(x)=cTxQuadratic f(x)=21xTQx+qTx,Q>0Norms (Any Norms) ∣x∣
Convex Optimization Problem
Generally, solving a convex optimization problem is minimizing a convex function over a convex sets.
Examples of Convex Optimization Problem:
Linear Program (LP) linear cost functionf(x)andlinear constraintsc(x)Quadratic Program (QP) quadratic cost functionf(x)andlinear constraintsc(x)Quadratically Constrained QP (QCQP) quadratic cost functionf(x)andelipsoid constraintsc(x)Second Order Cone Program (SOCP) linear cost functionf(x)andconic constraintsc(x)
In the Convex Optimization, there is no spurious local optima solution. Technically, if we manage to find the local optima Karush–Kuhn–Tucker (KKT) condition it will be our global solution.
Newton’s Method can work really well and converge really fast with 5~10 iterations (able to bound solution for the real-time control).
Written based on CMU Optimal Control Course 16-745.

